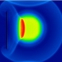
Имитационное моделирование теплопроводности
Имитационный подход к компьютерному моделированию отличается тем, что в нем отсутствуют математические модели, основанные на дифференциальных уравнениях изучаемых процессов. Имитационный подход хорошо зарекомендовал себя для решения определенного класса задач, когда возникают сложности при задании уравнений, либо сложности при решении уравнений (например, когда решение уравнений требует огромных вычислительных ресурсов).
В данной программе используется дискретная имитационная модель, относящаяся к классу так называемых клеточных автоматов. Все расчетное двумерное пространство делится на квадратные клетки (отсюда название «клеточный автомат»). Весь временной процесс моделирования поделен на отдельные временные шаги. На каждом временном шаге каждая клетка определяет свое новое состояние в зависимости состояний соседних клеток.
Имитационная модель, заложенная в эту программу, позволяет моделировать процессы твердотельной теплопроводности. Особенностью данной имитационной модели является то, что она может рассчитывать передачу тепла в материале со сложной пористой структурой. То есть появляется возможность исследовать изменение теплопроводящих свойств материала при появлении в нем той или иной пористой структуры. А ведь все теплоизолирующие материалы, в том числе и одежда, которую носит человек, являются материалами с большой пористостью.
То есть данная программа в основном нацелена качественное изучение процессов теплообмена в пористой среде с целью повышения уровня понимания школьниками физических основ процессов, связанных с теплообменом.
Описание математической модели, заложенной в программу
Поле клеток разбивается на отдельные блоки размером 2 на 2 клетки. При смене нечетного временного шага на четный шаг все блоки смещаются на одну клетку по горизонтали и вертикали.
На нечетном шаге
На четном шаге
Клетка может иметь значение единицы или нуля. На каждом временном шаге каждый блок ячеек с вероятностью 50% поворачивается на угол 90 градусов вправо или влево.
Ячейка со значением единица отображается красным цветом (красная частица), со значением нуль - черным. Если, например, нарисовать прямоугольную область красных частиц, то с течением времени красные частицы начинают блуждающее неупорядоченное движение по случайной траектории и рассеиваются в черном пространстве.
Математически строго доказано, что закон изменения концентрации частиц соответствует закону изменения температуры в процессе твердотельного теплообмена или диффузионному закону. Соответствие данной модели процессу реального теплообмена становится абсолютным при увеличении объема, в котором рассчитывается концентрация красных частиц. При уменьшении объема для расчета концентрации (объема осреднения) наблюдается увеличение стохастических отклонений от реального закона теплопроводности.
Трехмерный график температуры при объеме осреднения 20 на 20 ячеек
Трехмерный график температуры при объеме осреднения 10 на 10 ячеек (наблюдается стохастическое отклонение реального распределения температуры)
Степень концентрации частиц показывает температуру. Нулевая концентрация означает минимальную температуру, максимальная концентрация – максимальную температуру. Температуру в промежутке от минимальной до максимальной можно вычислить по формуле:
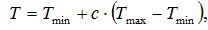
где с – концентрация частиц (от 0 до 1), то есть отношение количества красных частиц к общему числу клеток в объеме осреднения.
